苍茫大地的博客

日志

关于我

追逐

盒子里的梦想

文章分类

·默认分类（42）

sinc函数的作用(转载)

2012-02-07 12:21:27| 分类：默认分类 | 标签： |举报 |字号大中小订阅

下载LOFTER 我的照片书 |

技术与学术

Sinc滤波器

在信号处理领域，Sinc滤波器一个全部除去给定带宽之上的信号分量而只保留低频信号的理想电子滤波器。在频域它的形状象一个矩形函数，在时域它的形状象一个Sinc函数。由于理想的 Sinc 滤波器（人们熟知的矩形滤波器）有无限的延迟，所以现实世界中的滤波器只能是它的一个近似，但是它仍然在概念演示或者验证中得到了广泛应用，如采样定理以及Whittaker–Shannon插值公式。

矩形函数的定义为，

$\mathrm{rect}(t) = \sqcap(t) = \begin{cases} 0 & \mbox{if } |t| > \frac{1}{2} \\[3pt] \frac{1}{2} & \mbox{if } |t| = \frac{1}{2} \\[3pt] 1 & \mbox{if } |t| < \frac{1}{2} \end{cases}$

矩形函数

在数字信号处理和通信理论中，归一化sinc函数通常定义为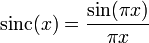

$\mathrm{sinc}(x) = \frac{\sin(\pi x)}{\pi x}$

在数学领域，历史上非归一化sinc函数 (for sinus cardinalis)定义为

$\mathrm{sinc}(x) = \frac{\sin(x)}{x}$

3 sinc

功能：产生Sinc或sin(πt)/ πt函数波形。

格式：y = sinc(x)

说明：sinc(x)用于计算sinc函数，即

Sinc函数之所以重要，是因为它的傅立叶变换正好是幅值为1的矩形脉冲。

补零对频谱的影响：
进行zero padding只是增加了数据的长度，而不是原信号的长度。就好比本来信号是一个周期的余弦信号，如果又给它补了9个周期长度的0，那么信号并不是10个周期的余弦信号，而是一个周期的余弦加一串0，补的0并没有带来新的信息。其实zero padding等价于频域的sinc函数内插，而这个sinc函数的形状（主瓣宽度）是由补0前的信号长度决定的，补0的作用只是细化了这个sinc函数，并没有改变其主瓣宽度。而频率分辨率的含义是两个频率不同的信号在频率上可分，也就要求它们不能落到一个sinc函数的主瓣上。所以，如果待分析的两个信号频率接近，而时域长度又较短，那么在频域上它们就落在一个sinc主瓣内了，补再多的0也是无济于事的。

评论这张

转发至微博

阅读(6684)| 评论(0)

历史上的今天

this.p={  m:2,
              b:2,
              loftPermalink:'',
              id:'fks_087067083094088069082082095071072094089066082094085065086',
              blogTitle:'sinc函数的作用(转载)',
              blogAbstract:'<IMG alt=\"sinc函数的作用(转载) - 追逐 - 苍茫大地的博客\"  title=\"此博文包含图片\"  src=\"http://simg.sinajs.cn/blog7style/images/common/sg_trans.gif\"  width=\"15\" align=\"absMiddle\" \><CITE\><IMG title=\"sinc函数的作用(转载) - 追逐 - 苍茫大地的博客\"  alt=\"sinc函数的作用(转载) - 追逐 - 苍茫大地的博客\"   src=\"http://simg.sinajs.cn/blog7style/images/common/sg_trans.gif\"  width=\"15\" align=\"absMiddle\" \></CITE\>  <TABLE\>  <TBODY\>  <TR\>  <TD\></TD\>  <TD\> <A target=\"_blank\" rel=\"nofollow\" href=\"http://blog.sina.com.cn/s/articlelist_1650196950_1_1.html\" \>技术与学术</A\> </TD\></TR\></TABLE\><BR\><BR\>Sinc滤波器<BR\>  <P style=\"TEXT-INDENT: 2em;\"  \>在<A rel=\"nofollow\" href=\"http://zh.wikipedia.org/wiki/%E4%BF%A1%E5%8F%B7%E5%A4%84%E7%90%86\"  \>信号处理</A\>领域，Sinc滤波器一个全部除去给定带宽之上的信号分量而只保留低频信号的理想</P\>',
              blogTag:'',
              blogUrl:'blog/static/8816832220121702127313',
              isPublished:1,
              istop:false,
              type:0,
              modifyTime:0,
              publishTime:1328588487313,
              permalink:'blog/static/8816832220121702127313',
              commentCount:0,
              mainCommentCount:0,
              recommendCount:1,
              bsrk:-100,
              publisherId:0,
              recomBlogHome:false,
              currentRecomBlog:false,
              attachmentsFileIds:[],
              vote:{},
              groupInfo:{},
              friendstatus:'none',
              followstatus:'unFollow',
              pubSucc:'',
              visitorProvince:'',
              visitorCity:'',
              visitorNewUser:false,
              postAddInfo:{},
              mset:'000',
              mcon:'',
              srk:-100,
              remindgoodnightblog:false,
              isBlackVisitor:false,
              isShowYodaoAd:false,
              hostIntro:'盒子里的梦想',
              hmcon:'1',
              selfRecomBlogCount:'0',
              lofter_single:'<iframe width="140" height="560" style="overflow:hidden;" src="http://www.lofter.com/mailEntry.do?blogad=1&blog" frameBorder="0"></iframe>'
            }

{list a as x}
    {if !!x}
    <div class="iblock nbw-fce nbw-f40">
      <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.visitorName}/">
      {if x.visitorName==visitor.userName}
      <img alt="${x.visitorNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.visitorName)}&r=${visitor.imageUpdateTime}"/>
      {else}
      <img alt="${x.visitorNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.visitorName)}"/>
      {/if}
      </a>
      <div class="cwd vname thide">
        {if x.moveFrom=='wap'}
          <a class="noul pnt" target="_blank" href="http://blog.163.com/services/wapblog.html?frompersonalbloghome"><span title="来自网易手机博客" class="iblock wapIcon"> </span></a>
        {elseif x.moveFrom=='iphone'}
          <a class="noul pnt" target="_blank"><span title="来自iPhone客户端" class="iblock iphoneIcon"> </span></a>
        {elseif x.moveFrom=='android'}
          <a class="noul pnt" target="_blank"><span title="来自Android客户端" class="iblock androidIcon"> </span></a>
        {elseif x.moveFrom=='mobile'}
          <a class="noul pnt" target="_blank" href="http://blog.163.com/services/emsblog.html?frompersonalbloghome"><span title="来自网易短信写博" class="iblock wapIcon"> </span></a>
        {/if}
        <a class="fc03 m2a"  target="_blank" hidefocus="true" href="http://blog.163.com/${x.visitorName}/">
          ${fn(x.visitorNickname,8)|escape}
        </a>
      </div>
    </div>
    {/if}
    {/list}

<#--最新日志，群博日志--> <#--推荐日志-->

<p class="fc06">推荐过这篇日志的人：</p>
    <div>
      {list a as x}
      {if !!x}
      <div class="iblock nbw-fce nbw-f40">
        <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.recommenderName}/">
        <img alt="${x.recommenderNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.recommenderName)}"/>
        </a>
        <div class="cwd thide">
          <a class="fc03 m2a" target="_blank" hidefocus="true" href="http://blog.163.com/${x.recommenderName}/">
            ${fn(x.recommenderNickname,6)|escape}
          </a>
        </div>
      </div>
      {/if}
      {/list}
    </div>
    {if !!b&&b.length>0}
    <p  class="fc06">他们还推荐了：</p>
    <ul>
    {list b as y}
      {if !!y}
        <li class="rrb"><span class="iblock">·</span><a class="fc03 m2a" target="_blank" href="http://blog.163.com/${y.recommendBlogPermalink}/?from=blog/static/8816832220121702127313">${y.recommendBlogTitle|escape}</a></li>
      {/if}
    {/list}
    </ul>
    {/if}

<#--引用记录--> <#--博主推荐--> <#--随机阅读--> <#--首页推荐--> <#--历史上的今天--> <#--被推荐日志--> <#--上一篇，下一篇--> <#-- 热度 -->

{list a as x}
    {if !!x}
    <div class="hotItem iblock nbw-fce nbw-f40">
      <a class="fc03 noul" target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/">
      {if x.publisherUsername==visitor.userName}
      <img alt="${x.publisherNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.publisherUsername)}&r=${visitor.imageUpdateTime}"/>
      {else}
      <img alt="${x.publisherNickname|escape}" onerror="this.src=location.f40" class="cwd bdwa bdc0" src="${fn1(x.publisherUsername)}"/>
      {/if}
      </a>
      <div class="cwd vname thide">
        <a class="fc03 m2a"  target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/">
          ${fn(x.publisherNickname,8)|escape}
        </a>
      </div>
      <a class="f-myLikeIcons hottype {if x.type==1} js-liketype{elseif x.type==2} js-reblogtype{elseif x.type==3} js-sharetype{else}{/if}" target="_blank" hidefocus="true" href="http://blog.163.com/${x.publisherUsername}/"> </a>
    </div>
    {/if}
    {/list}

<#-- 网易新闻广告 --> <#--右边模块结构--> <#--评论模块结构--> <#--引用模块结构--> <#--博主发起的投票-->

页脚

我的照片书 - 手机博客 - 下载LOFTER APP - 订阅此博客

苍茫大地的博客

导航

日志

sinc函数的作用(转载)

历史上的今天

最近读者

热度

评论

页脚